A colleague approached me a while ago and asked me a question about Kotlin. What was this “Nothing type”, and what was it used for? I did not really have a good answer for him at the time. Since then, I’ve found my answer.

Nothing Type is the Bottom Type

In mathematics, bottom (often denoted as _|_) represents the absolute minimum value something can hold.

Nothing type has no instances. You can use Nothing to represent “a value that never exists”: for example, if a function has the return type of Nothing, it means that it never returns (always throws an exception).

Previously shared Kotlin post:

1. Top 12 Advanced Kotlin Tips For Pro Developers
2. Kotlin Parcelize – Developer need to know
3. Create Firefox Extension Using KotlinJS

When we’re talking about types, we can think of Nothing as being the absolute bottom (leaf) object of any type hierarchy.

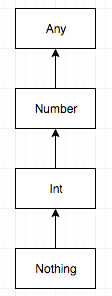
What we can see in this diagram (figure 1) is that Nothing is the opposite of Any. While every object you will work with in Kotlin implicitly extends Any, so to does Nothing implicity extend any object that exists. This makes Nothing the ‘dual’ or opposite of Any.

So, why is this useful?

Covariant Types (an Example)

We can use Nothing along with covariant (producer) types to help make our code more concise and expressive. The following is an example of the Nothing type in action. It is of an Either monad, which can exclusively represent one of two types (L or R), and provides methods for mapping over the values it wraps, including a right-biased map and flatMap (by convention) and a very useful either method.

// Composes 2 functions
fun <A, B, C> ((A) -> B).c(f: (B) -> C): (A) -> C = {
    f(this(it))
}

// A simple Either monad
sealed class Either<out L, out R> {
    data class Left<out L>(val a: L) : Either<L, Nothing>()
    data class Right<out R>(val b: R) : Either<Nothing, R>()

    val isRight: Boolean
        get() = this is Right<R>

    val isLeft: Boolean
        get() = this is Left<L>
}

fun <L> left(a: L) = Either.Left(a)
fun <R> right(b: R) = Either.Right(b)

fun <T, L, R> Either<L, R>.flatMap(fn: (R) -> Either<L, T>): Either<L, T> =
        when (this) {
            is Either.Left -> Either.Left(a)
            is Either.Right -> fn(b)
        }

fun <T, L, R> Either<L, R>.map(fn: (R) -> (T)): Either<L, T> = this.flatMap(fn.c(::right))

fun <T, L, R> Either<L, R>.either(fnL: (L) -> T, fnR: (R) -> T): T =
        when (this) {
            is Either.Left -> fnL(a)
            is Either.Right -> fnR(b)
        }

Covariance (marking our parameters as out) allows us to utilize nothing in the R and L positions of the Left and Right declarations of the Eithermonad implemented here (respectively). Our functions all typecheck and are happy. For example, something like:

val e = right(42).flatMap(r -> left(Exception())

Will happily type-check and compile. We can even rigidly express the type of e and it’s still happy as can be, all thanks to Nothing and covariance:

val e: Either<Int, Exception> = right(42)
    .flatMap { left(Exception() }

You might have noticed that extension methods are being used here for map, flatMap, and so on. This is due to the Covariant typing mentioned above, which produces type-check errors when trying to pass a lambda utilizing the generic types. Extension methods are a quick and easy way around this issue.

So what did we actually get?

What we end up with is a better, more concise way to express our types. Nothing almost acts like a type hole, similar to utilizing _ in lambda arguments. We can use it in places where we really just don’t care about the type of something. In our case, if we’ve got a Right, we don’t really need to know anything about the error, because it doesn’t exist. On the other hand, if we have a Left, knowledge of the error is necessary, but not so much for the normal value.

Hopefully this sheds some light on why Nothing exists and how it can be leveraged.